Bem-vindo à segunda parte da nossa série de artigos sobre Engenharia Reversa Básica! Link para o cabeçalho
██ ██ █████ ██████
██ ██ ██ ██ ██
███ █████ ███████
██ ██ ██ ██ ██ ██
██ ██ █████ ██████
Agora que já exploramos os conceitos fundamentais de CPU no primeiro artigo, chegou a hora de entender como os dados são representados e manipulados internamente pelos computadores. Vamos falar sobre sistemas de numeração, com foco em hexadecimal, que é crucial para quem trabalha com engenharia reversa em baixo nível.
No nosso primeiro artigo, eu disse — Não se prenda a uma sequência infinita de “porquês!?”. E digo novamente: Não se preocupe em entender todos os detalhes de uma vez. O objetivo aqui é entender a essência dos conceitos e como cada um contribui para o funcionamento do sistema computacional. A ideia não é se perder em explicações técnicas, mas sim entender como tudo se encaixa, e isso irá ficar muito claro na prática futuramente.
Sistema Binário Link para o cabeçalho
O sistema binário é a linguagem dos computadores. é um sistema de numeração que utiliza apenas dois símbolos, como estados de interruptor: 0 -> desligado e 1 -> ligado. Ele é a base da computação, e razão para isso é que: os computadores, em seu nível mais profundo, funcionam com circuitos elétricos que podem estar em dois estados distintos: ligado ou desligado. O 0 e o 1 são a maneira de representar esses estados binários. Por debaixo dos panos, o sistema é isso:
0001010101011010101011100101010010101010...
Mas, obviamente, nós não temos contato direto com isso e nem vemos esse binário. Isso é processado pelas camadas de abstração, como: circuitos, CPU, sistema operacional e diversas outras partes que formam o computador, que tratam dos binários para nós.
Para a formação de caracteres e números, os bits se repetem, assim como em qualquer outro sistema numérico.
- 1 bit pode representar 2 valores: 0 ou 1.
- 2 bits podem representar 4 valores: 00, 01, 10 e 11.
- 3 bits podem representar 8 valores: 000, 001, 010, 011, 100, 101, 110 e 111. E assim por diante…
No sistema operacional, tudo é representado por binários. Cada sequência binária pode representar algo específico: pode ser uma tecla de escape, uma tecla de espaço, uma entrada, uma saída, um número, uma letra, e por aí vai. Tudo tem um significado codificado em binário.
Você pode ver na tabela ASCII como as saídas de texto são representadas em binário.
- Aqui está um exemplo dessa tabela.
Características do Sistema Binário Link para o cabeçalho
- Base 2: O sistema binário é composto por dois símbolos: 0 e 1.
- Assim como qualquer outro sistema numérico, como o decimal (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), o sistema binário usa dois dígitos. Com apenas esses dois símbolos, podemos representar números infinitos, basta reorganizá-los de maneiras diferentes.
- Posicional: Cada dígito tem um valor que depende da sua posição na sequência. Isso ocorre porque o sistema é posicional e de base 2, ou seja, a posição de cada bit define seu valor.
- Armazenamento de Dados: Discos rígidos, SSDs, memórias RAM e outros dispositivos de armazenamento utilizam o sistema binário para armazenar informações. Cada bit é uma cadeia, que representa dados, e esses dados são interpretados pelo sistema operacional.
- Representação de Dados: Todos os dados e instruções em um computador são representados em binário. Isso inclui texto, imagens, vídeos, programas e qualquer outro tipo de informação. Até as instruções que a CPU executa são representadas em binário, e são interpretadas conforme o contexto.
- Representação: No sistema operacional, ele é representado por 0b, ou seja: 0b1100110.
Conclusão Link para o cabeçalho
Embora o sistema binário seja fundamental para a computação, você provavelmente não precisará ter contato diretamente no seu dia a dia. No entanto, entender como ele funciona é importante, pois, no futuro, você pode precisar de algum conhecimento básico sobre binários para compreender outros conceitos relacionados à engenharia reversa.
Recursos Auxiliares Link para o cabeçalho
- Binary to Decimal – Brinque com números binários e veja como eles funcionam.
- Mente Binária - Cálculos com Binários – Aprenda a fazer cálculos binários, caso queira se aprofundar(recomendável).
Hexadecimal Link para o cabeçalho
Bom, agora iremos falar sobre o Hexadecimal. Acredito que seja o sistema numérico mais utilizado pra quem faz engenharia reversa, ao lidarmos com endereços de memória e manipulação de dados de baixo nível, o sistema hexadecimal é muito mais compacto e legível do que o sistema binário.
O sistema hexadecimal é de base 16, o que significa que ele usa 16 símbolos diferentes para representar valores. Esses símbolos são:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Números de 10 a 15 são representados por letras:
- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15
... 8, 9, A, B, C, D, E, F, 10, 11, 12...
10 equivale a 16 e assim por diante…
Como funciona a Numeração Hexadecimal Link para o cabeçalho
Assim como no sistema decimal, onde cada posição representa uma potência de 10, em hexadecimal a potência corresponde à posição de cada número no sistema hexadecimal.
Potências de 16 de 0 até 5: Link para o cabeçalho
| (16⁰) |
(16¹) | (16²) | (16³) | (16⁴) | (16⁵) |
|---|---|---|---|---|---|
| 1 | 16 | 256 | 4.096 | 65.536 | 1.048.576 |
Vamos ao exemplo:
No número 2F (hexadecimal):
- 2 ocupa segunda posição à esquerda:
- 2 x 16¹ = 2 x 16 = 32
- F ocupa a primeira posição à esquerda:
- F representa 15 em decimal, então:
- 15 x 16⁰ = 15 x 1 = 15
Portanto, 2F (hexadecimal) é igual a 32 + 15 = 47 em decimal.
Vamos a outro exemplo, o número: 0x543210
- 5(16⁵) x 1.048.576 = 5.242.880
- 4(16⁴) x 65.536 = 262.144
- 3(16³) x 4.096 = 12.288
- 2(16²) x 256 = 512
- 1(16¹) x 16 = 16
- 0(16⁰) x 1 = 0
A potência de cada número indica quantas vezes ele deve ser multiplicado pelo valor correspondente da posição.
Resultado Link para o cabeçalho
Agora, vamos somar esses valores para obter o número decimal de 0x543210:
5.242.880+262.144+12.288+512+16+0 = 5.517.840
Então, 0x543210 é igual a 5.517.840 em decimal.
Inserindo letras Link para o cabeçalho
podemos também inserir letras nos números hexadecimais. aprendemos acima que as letras A a F representam os valores de 10 a 15, portanto vamos usar o número 0xAB2345 como exemplo, e converter de hexadecimal para decimal:
Não se esqueça que: A =10 B = 11
- A(16⁵) x 1.048.576 = 10.485.760
- B(16⁴) x 65.536 = 720.896
- 2(16³) x 4.096 = 8.192
- 3(16²) x 256 = 768
- 4(16¹) x 16 = 64
- 5(16⁰)x 1 = 5
(AB2345)₁₆ = (10 × 16⁵) + (11 × 16⁴) + (2 × 16³) + (3 × 16²) + (4 × 16¹) + (5 × 16⁰) = (11215685)₁₀
somamos o resultado, e obtemos: 11.215.685.
Portanto, 0xAB2345 é 11.215.685 em decimal.
Legal, né?
Recursos Adicionais: Link para o cabeçalho
Hexadecimal nos Sistemas Operacionais Modernos Link para o cabeçalho
Bom, essa matemática toda por trás dos hexadecimais não será necessária, pois quem lida com isso é o sistema operacional. Mas há algumas coisas que você deve saber/lembrar quando for programar, fazer engenharia reversa ou coisas do tipo. Aqui vão elas:
- Em um sistema operacional moderno, 1 número em hexadecimal equivale a um número binário de 4 dígitos (4 bits). Por exemplo:
1101 = D
0001 = 1
0110 = 6
0011 = 3
-
Nos sistemas modernos como windows e linux, usamos o prefixo 0x, por exemplo
0xD163 -
Endereços dinâmicos de memória são representados em hexadecimal.

- Endereços estáticos/offsets de memória são representados por hexadecimal

- Dados são representados em hexadecimal.
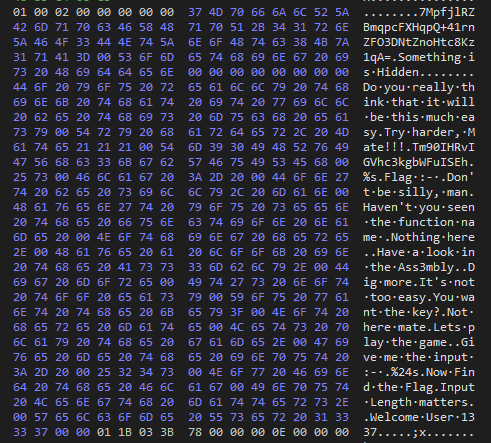
- Quando formos aplicar engenharia reversa, iremos lidar com números hexadecimais.
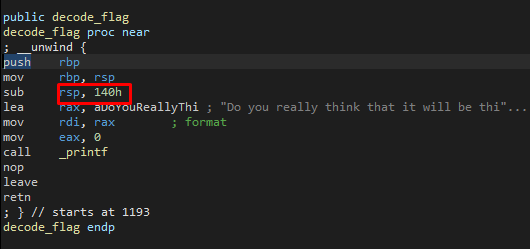
Resumindo, o hexadecimal é muito importante, pois está presente em tudo.
x86 Byte, Word, Double Word Link para o cabeçalho
Bom, essas são as nomenclaturas para a quantidade de dados que um determinado segmento armazena.
| Medida | Tamanho (Intel) | Nomenclatura Intel |
|---|---|---|
| Byte | 8 bits | BYTE |
| Word | 16 bits | WORD |
| Double Word | 32 bits | DWORD |
| Quad Word | 64 bits | QWORD |
Quando formos programar ou analisar um source code de um malware, iremos lidar com essas nomenclaturas, principalmente ao lidarmos com a WINAPI.
É importante, pois, por exemplo, se você declara uma variável do tamanho DWORD, você irá armazenar um valor de 32 bits:
DWORD procid = NULL;
Os registradores equivalem a esses tamanhos também. Veja:
AX= 16 bits (WORD)EAX= 32 bits (DWORD)RAX= 64 bits (QWORD)
Bom, a partir daqui é isso. O restante a gente aprende com a prática. Portanto pratique ao máximo, e esses conceitos irão entrar na sua mente.
Obrigado por ter lido até aqui!
▌ ▐· ▪ ▪ ·▄▄▄▄
▪█·█▌▪ ██ ██ ██▪ ██
▐█▐█• ▄█▀▄ ▐█·▐█·▐█· ▐█▌
███ ▐█▌.▐▌▐█▌▐█▌██. ██
. ▀ ▀█▄▀▪▀▀▀▀▀▀▀▀▀▀▀•